PRIVACY. Our most fundamental right. The thing that makes us secure on the internet. The reason why we have our identity safe, possibly, from exploitation and breach, if not fully. The reason why our communications are safe and secure. But ever wondered where does privacy fundamentally come from? Or, what makes a strong password "strong"? The answer lies in the realm of cryptography. Cryptography is the reason why all encryption, security and privacy exist.
What's Cryptography?
So, let's start with what even is cryptography, and why the heck does it even matter. Think about it this way, it's like turning information into something that's non-meaningful and gibberish for a person other than the person to whom the information is intended to be sent, ensuring the privacy of the individuals. That's one way of thinking about it. This gibberish is often referred to as cipher-text in technical terms, which means nothing meaningful can be interpreted just from it. The more random this ciphertext gets, the harder it becomes to decode this gibberish. It's also true for "strong" passwords, like how do we even quantify the security of a password? It's by measuring the amount of randomness in it. But the quantifiable property associated with randomness is Entropy, measured in bits. The higher the bits of entropy, the more random the ciphertext, the more random and strong the password.
Another important concept in the topic of cryptography is hash functions, which are designed to generate a unique fixed-size output, known as a hash value or digest, from any given input data. These hash values act as digital fingerprints, providing a reliable way to confirm that the original data has not been altered or tampered with during transmission or storage. In this sense, hash functions complement encryption by adding an extra layer of assurance and reliability to the security of digital communications. We'll get to the why and how of hash functions in the next section.
Hash Functions
They are one-way functions that produce a random unique fixed-size output(called the hash or the digest) by taking an input. Finding the input from the output is computationally infeasible, and for 2 different inputs, there cannot be the same output.

But why should we care? Firstly, hash functions provide data integrity. By generating unique hash values for specific inputs, they enable the detection of even the slightest modifications to the original data, because even a slightly altered input would result in a completely different hash value. This property is particularly useful in verifying the integrity of files, ensuring that they have not been tampered with or corrupted. For example, git uses the SHA1 hash function to produce a hash which is a unique identifier for a commit.
Moreover, hash functions are vital in password storage. Instead of storing passwords directly, systems typically store the hash values of passwords. This approach adds an extra layer of security by ensuring that even if the stored data is compromised, the original passwords remain hidden. When a user logs in, their entered password is hashed and compared against the stored hash value, allowing for secure authentication.
Key Derivation Functions
Key Derivation Functions(KDFs) are similar to hash functions except that they have one extra property, that is they are much slower to compute. This can be particularly useful to prevent brute-force attacks. Let's say a website has its password database stolen and somebody's going through all the accounts to break all the passwords. In that case, one would want the process to be slowed down to prevent the attacker from completing the brute force attack.
Now, it's finally time to get into the 2 most essential paradigms of cryptography, symmetric and asymmetric key cryptography.
Symmetric Key Cryptography
It uses a single key to encrypt and decrypt information. It uses 3 primary functions :
The keygen() function: generates the key(for encryption/decryption)
encrypt(plaintext, key): generates the ciphertext using key
decrypt(ciphertext, key): generates the original plaintext from the ciphertext using key

The keygen() function is randomized to generate the random key, which is used for both encrypting the plaintext(original input) to ciphertext and decrypting the plaintext from the ciphertext.

Symmetric key cryptography is most useful in scenarios where two entities already share a secret key. It enables secure communication by allowing encryption and decryption of messages using the shared key. This approach is efficient and doesn't require complex key exchange protocols. However, securely distributing and managing the shared secret key is crucial for maintaining the confidentiality of the communication. The process of securely distributing the secret key itself is where asymmetric key cryptography may come into play, both of which combined are responsible for end-to-end encryption.
Asymmetric Key Cryptography
Instead of a single shared key, we have a keypair here, consisting of a public and a private key.
keygen() → (public key, private key)
encrypt(plaintext, public key) → ciphertext
decrypt(ciphertext, private key) → plaintext
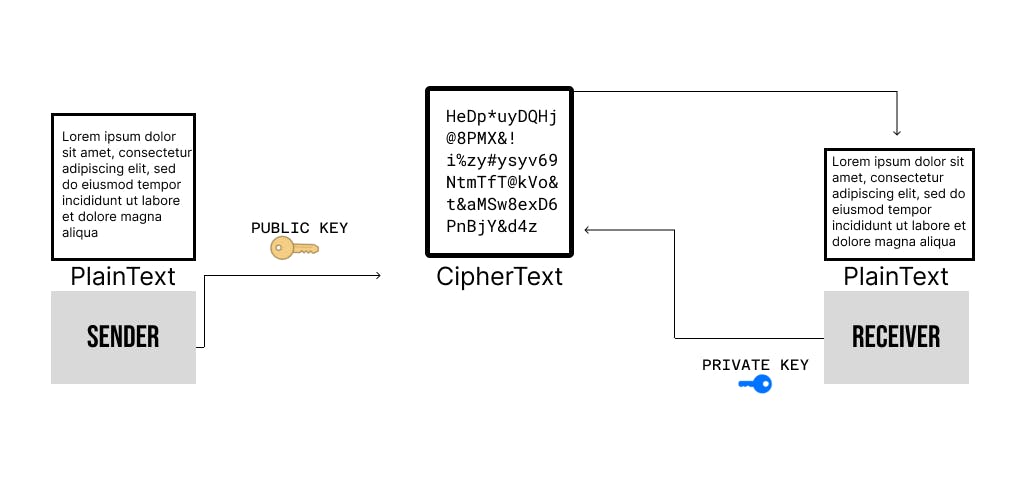
the keygen() function generates 2 keys, a public and a private key. The public key is used to encrypt the plaintext while the encrypted ciphertext can ONLY be decrypted using the private key. The public key is available to anyone who wants to encrypt the information, but the private key is only available to the recipient to whom the message is meant to sent, so that only the recipient could decrypt it. This is where the asymmetric part and the con of symmetric key cryptography come in. In case of symmetric, if the key is made public, then basically anyone could potentially encrypt and decrypt the information, killing privacy. That's why it was limited to 2 member systems. But here, the private key is only made available to the sender/receiver to whom this information is meant to be sent.
Signing and Verification
Signing and Verification are one of the most common use-cases of asymmetric key cryptography. Here, we use the sign() function to sign a message with a digital signature, and then use verify() function to check if the digital signature is valid or not.
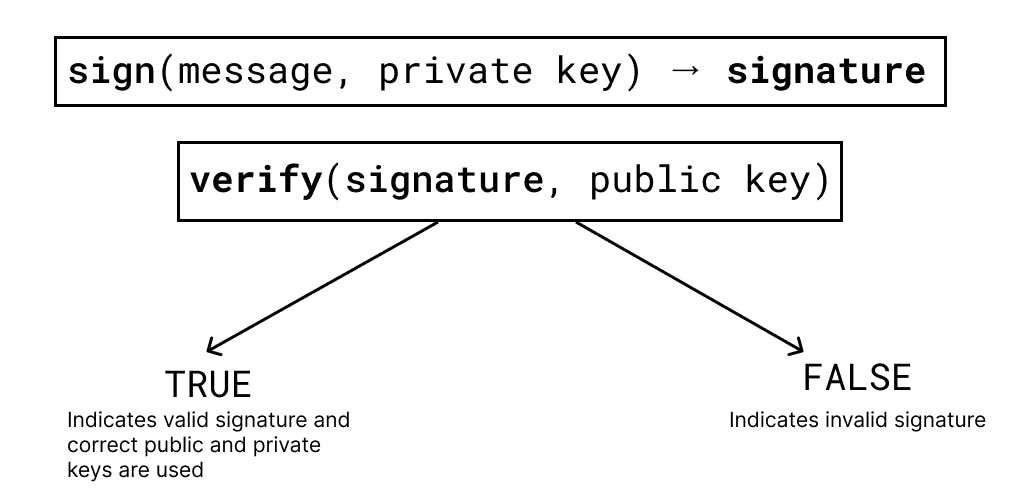
- The recipient checks the return value of the
verify()function to determine whether the signature is valid or not.
Applications
Secure key exchange protocols, like Diffie-Hellman, leverage asymmetric key cryptography to establish a shared secret key over an insecure channel. Secure email communication and web browsing utilize public-key certificates to authenticate the identity of the communication parties. Online transactions use asymmetric public-key cryptography to encrypt sensitive data, protecting it during transmission. In secure remote access, asymmetric key cryptography enables authentication and encrypted communication between the client and server. In summary, the applications of asymmetric key cryptography are directly tied to its working principles, where the use of public and private key pairs ensures confidentiality, integrity, and authentication in various secure communication scenarios.
Culmination
So... is it the end? No! These were some of the fundamentals of cryptography for you to realize how intrinsic it is to everything you do today on the internet! It's an entire universe consisting of many different areas and topics that you could explore on your own. But but... there is a concern. A Major One. The majority of the encryption algorithms used today, like RSA, ElGamal, Diffie-Hellman Key Exchange, to name a few, rely on one-way key generation functions for working. They might be computationally infeasible and near impossible to break today, but with the advent of quantum computers coming, in the next 10-20 years, it might become very possible to completely break these encyption algorithms and boom, privacy becomes a forbidden concept. THESE QUANTUM COMPUTERS CAN BE THE BIGGEST THREAT TO PRIVACY IN THE FUTURE.
In most cases, these encryption algorithms depend on the difficulty of certain computationally intensive mathematical problems, such as factoring large numbers(as in case of RSA) or solving discrete logarithm problems, which form the basis of their security. Classical computers require a significant amount of time and computational resources to solve these problems, making the encryption secure against conventional attacks. This is exactly where quantum computers would come into play. Performing those computations would be a matter of minutes, or even seconds, if given a quantum computer powerful enough.
Some nation-states are already storing lots of encrypted data like passwords,bank-details,etc. because they believe that in the near future they would have access to those quantum computers, and that information would still be valuable to them then. This is known as Store Now, Decrypt Later(SNDL). Recently,the US Congress just passed legislation mandating all agencies to start transitioning to new methods of quantum-resistant cryptography algorithms.
So, would we be able to completely transition to quantum-resistant cryptography algorithms till the advent of quantum computing occurs? Would ALL Secrets, as they exist today, remain encrypted EVEN AFTER the next 20 years? ONLY TIME WOULD TELL!